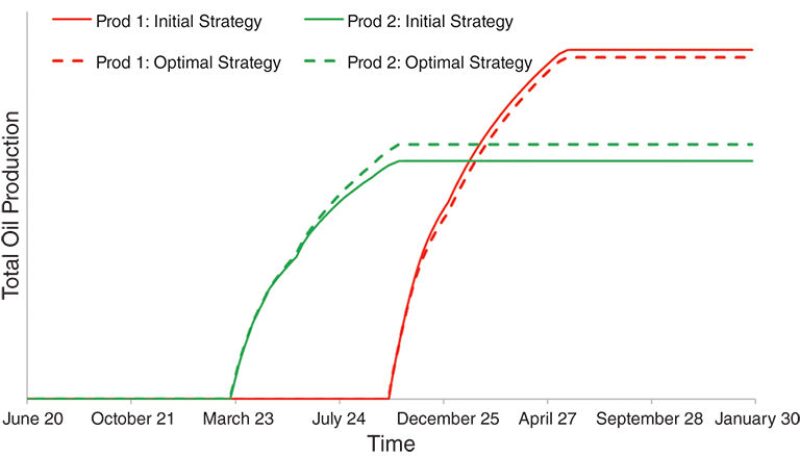
The growing popularity of model-based optimization work flows has resulted in an increase in their application to field cases. In the complete paper, the authors present the challenges, results, and learnings from a 2-year robust multiobjective optimization application at the Mariner heavy-oil asset in the UK sector of the North Sea. The authors used the efficient stochastic simplex approximate gradient technique (StoSAG) to achieve optimization incorporating geological and petrophysical uncertainty. Depending on the problems, significant increases of between 5 and 20% in the expected value of the objective function were achieved.
×


Continue Reading with SPE Membership
SPE Members: Please sign in at the top of the page for access to this member-exclusive content. If you are not a member and you find JPT content valuable, we encourage you to become a part of the SPE member community to gain full access.