Many two-phase and three-phase separators in the oil and gas industry continue to underperform. Sometimes, the wrong type of equipment was selected, or the correct type of equipment was selected, but the sizing methodology was inadequate.
There is a wide range of sizing methods for two-phase separators, varying from the simple “back-of-the-envelope” to the far more complicated.
There are several weaknesses associated with most of these methods, including:
- Quantification of feed flow steadiness
- Entrainment/droplet size distribution quantification
- Velocity profile/distribution quantification
- Separator component performance quantification
This article explores the weaknesses and proposes manageable approaches to quantifying each. The intent is to develop a more consistent approach to separator sizing and reduce the level of empiricism typically employed in the past.
The equations in this article were incorporated into a Microsoft Excel spreadsheet, using Microsoft’s Solver add-in to optimize separator dimensions when given the operating conditions, a set of constraints, and the target separation efficiency specifications.
Separation Equipment
Separation equipment can be classified in various ways: two-phase or three-phase, vertical or horizontal, and other categories. In the two-phase (gas/liquid) category, an additional breakdown of equipment can be made: slug catcher→conventional separator→scrubber→coalescing filter.
This article focuses on scrubbers and conventional separators.
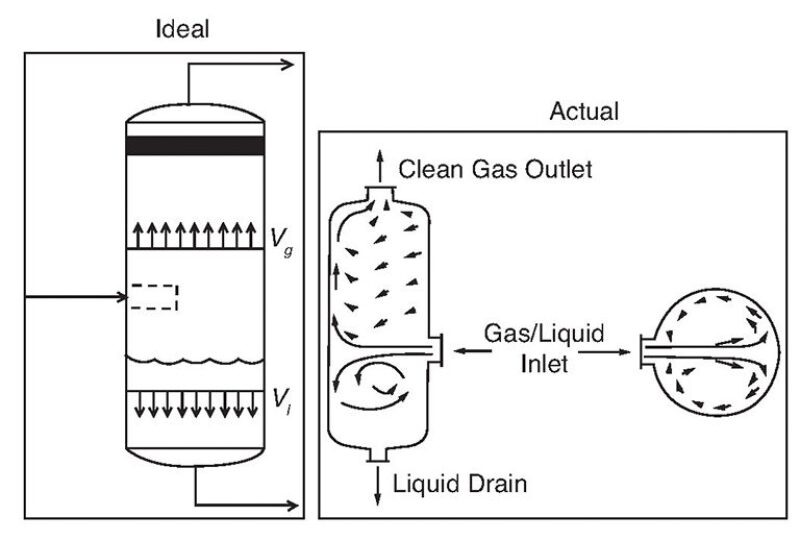
The major parts of a separator (Fig. 1) are the feed pipe, inlet device, gas gravity separation section, mist extractor, and the liquid gravity separation section. Each of these parts will be discussed, with the objective of quantifying their effects on gas/liquid separation performance as measured by the quality of the separated fluid phases. The quality is defined by how much liquid remains in the separated gas, and how much gas remains in the separated liquid.
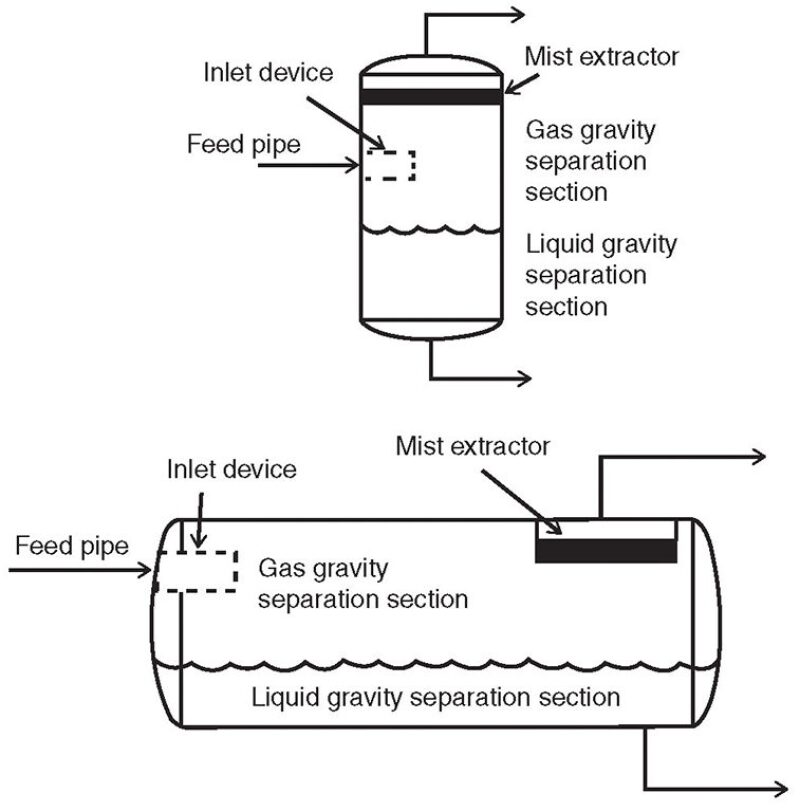
The quality of the separated gas phase is an indicator of separation efficiency. In the author’s experience, operational problems associated with too much liquid in the gas are far more prevalent than those caused by too much gas in the liquid. On the liquid-handling side, the more common issue is how best to deal with intermittent (slugging) flow.
Feed Pipe
The significance of the sizing and geometry of a separator’s feed pipe has only recently been quantified. The main objective of most types of separation equipment is to remove droplets of a dispersed phase from a second continuous phase. A secondary requirement is often for the separator to have some capability to deal with intermittent flow (slugging).
The following questions are important in the sizing and performance prediction of most types of separation equipment, including the individual components:
- What is the flow pattern at the separator’s inlet?
- How much of the dispersed phase (liquid droplets) is present in entrained form?
- What are the sizes of the droplets?
Unfortunately, quantification of these values is difficult and typically requires simplifying assumptions. The validity of these assumptions has a significant bearing on equipment selection, sizing, and performance prediction.
Flow Pattern
Fig. 2 provides a visual classification of the flow patterns most commonly encountered in horizontal two-phase flow. In general, the flow pattern is primarily dependent on the relative amounts of gas and liquid in the feed pipe and the in-situ phase velocities.
Fig. 3 is a commonly used horizontal flow pattern map (Mandhane 1974) corresponding to Fig. 2. The horizontal axis parameter is the superficial gas velocity, while the vertical axis parameter is the superficial liquid velocity. Superficial velocity is defined as the in-situ (actual) volumetric flow rate of the given fluid phase divided by the total cross-sectional flow area of the pipe.
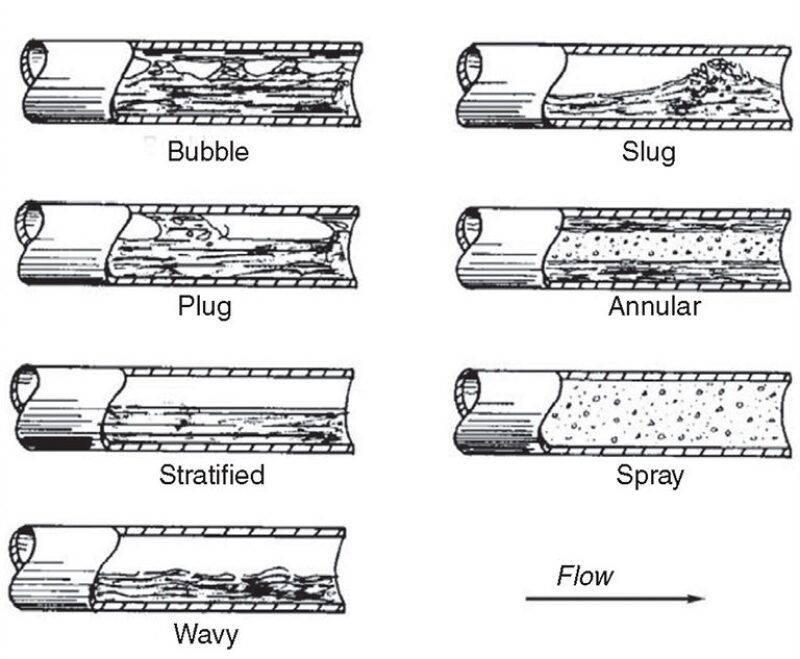
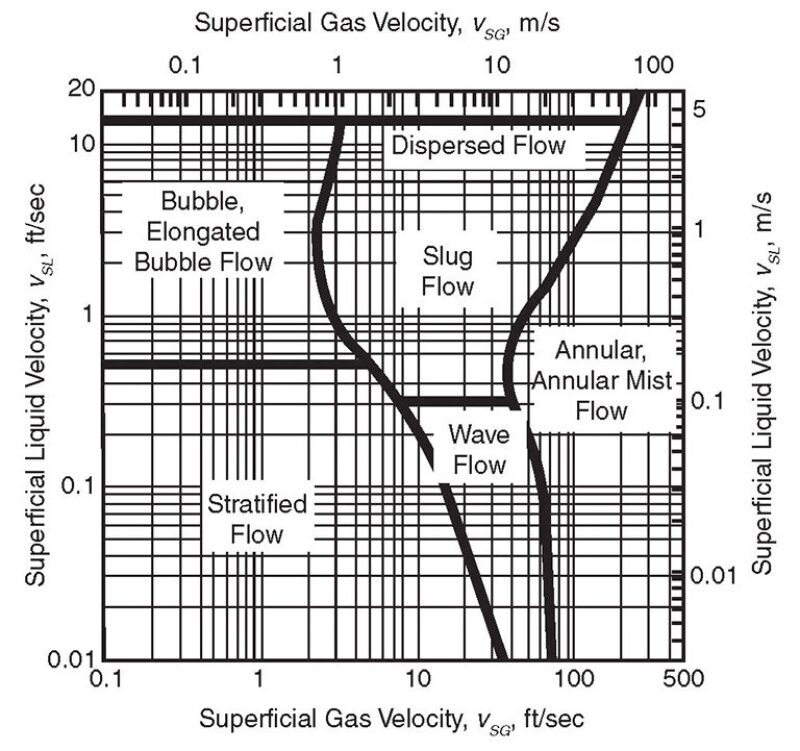
The amount of liquid entrained into the gas phase as droplets is generally small for most flow conditions, but will typically begin to increase fairly rapidly as the transition to annular flow is approached. From the standpoint of the amount of liquid droplets entrained into the gas phase, it seems fairly obvious that the annular mist region of the flow pattern map will be the worst. Generally speaking, increasing gas velocity is going to strongly correlate with the increasing entrainment and with decreasing droplet sizes, both of which will negatively affect separation. Taking into account both entrainment/droplet sizes and steadiness of flow, sizing the feed pipe for stratified/wave flow is desirable, if possible.
Feed Pipe Geometry
The flow patterns and flow pattern map assume that the flow conditions in the feed pipe have reached a well-established, stabilized state. This will not be true if the flow has changed direction, for example, at elbows and fittings, or experienced other flow pattern disruptions immediately upstream of the separator.
Typical guidelines are:
- Provide 10 diameters of straight pipe upstream of the inlet nozzle without valves, expansions/contractions, or elbows.
- If a valve in the feed line near the separator is required, it should only be a full port gate or ball valve.
Entrainment
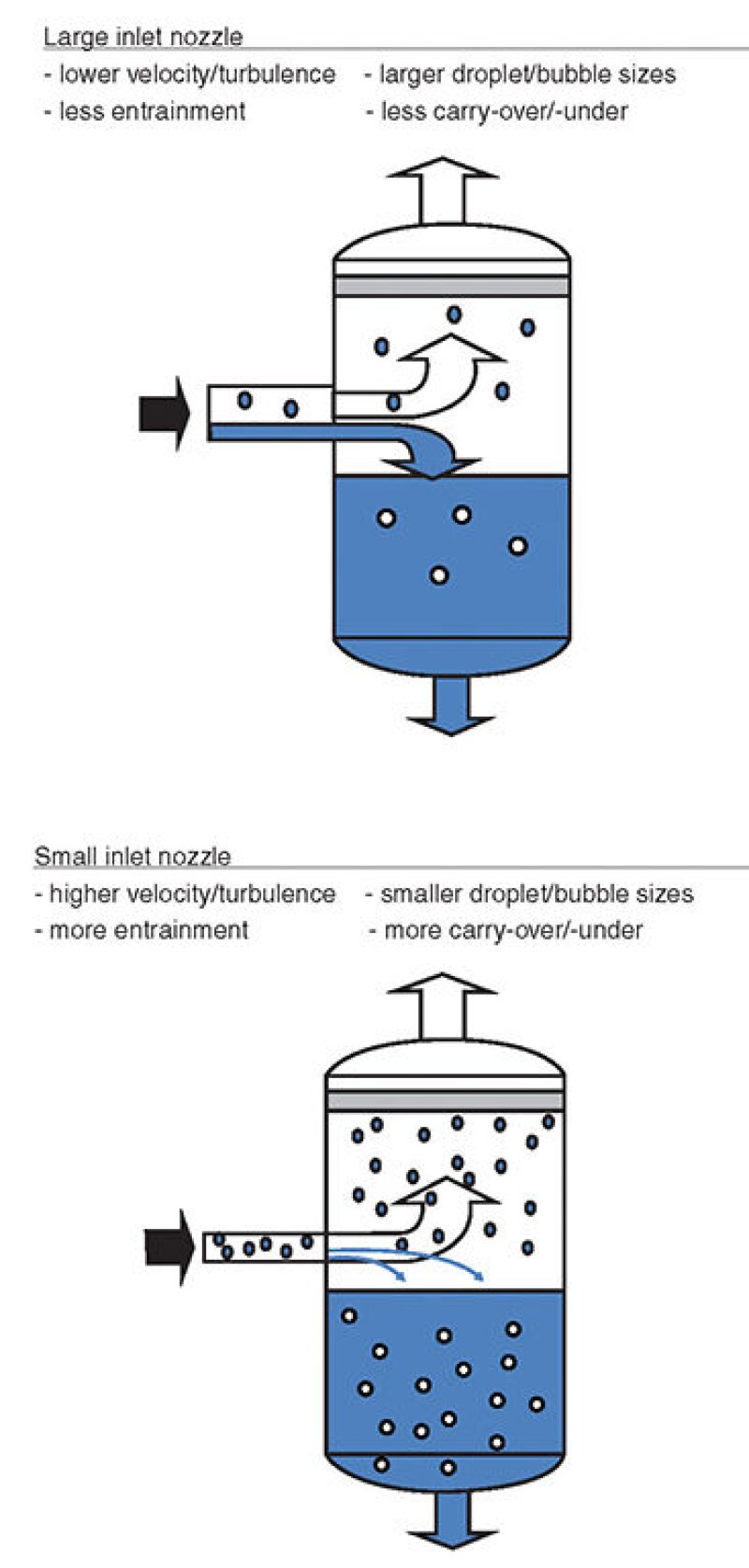
The amount of liquid entrained as droplets entering the separator will have a significant effect on the gas/liquid separation performance and, ultimately, the amount of liquid carry-over into the gas phase leaving the separator (Fig. 4).
Ishii and Grolmes (1975) identified the causes of liquid entrainment in gas/liquid systems and provided guidelines for estimating entrainment inception criteria (Fig. 5). The applicable entrainment mechanism for a given set of conditions is strongly dependent on the liquid phase Reynolds number.
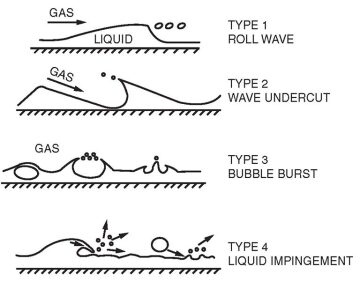
For many separation applications, the main liquid entrainment mechanism is the shearing off of roll-wave crests (Fig. 5, Type 1). The onset of entrainment by this mechanism would be expected to coincide approximately with the wavy/annular transition shown in Fig. 3 and approximately with the transition from slug flow to annular flow.
Estimating the amount of liquid entrained as droplets into the gas phase is difficult and one of the main causes of uncertainty involved in sizing of separators and performance prediction.
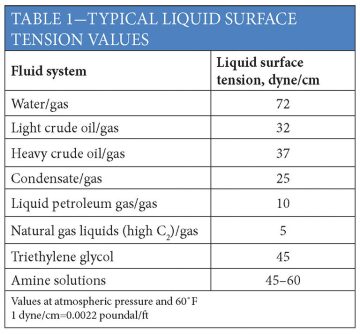
The degree of liquid entrainment is a function of the following variables (among others):
• Entrainment increases with increasing velocity.
• Entrainment increases with decreasing liquid surface tension.
Pan and Hanratty (2002) have developed a correlation for predicting liquid droplet entrainment for annular flow in horizontal pipes. For nonannular (lower velocity) flow, the predicted entrainment fraction decreases toward zero.
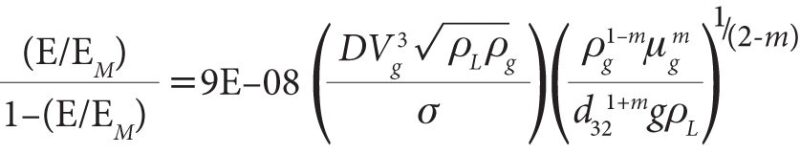
............................................... (1)
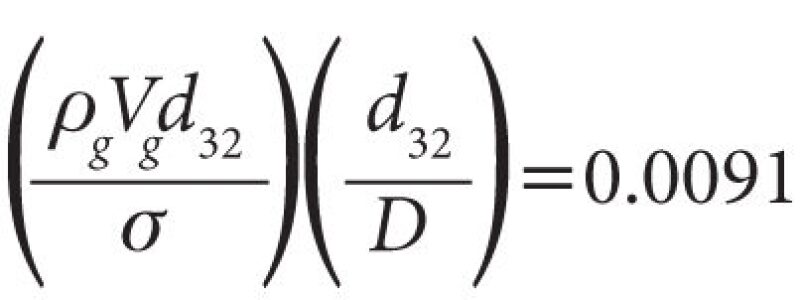
............................................................................................... (2)
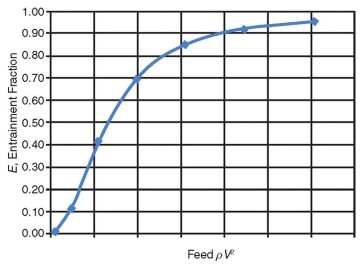
Fig. 6 shows a typical plot of liquid entrainment fraction (E) vs. inlet momentum (ρV2). Note that after the entrainment inception point is reached, the degree of entrainment increases rapidly.
Droplet Sizes and Distribution
The Pan and Hanratty correlation includes a method for estimating the Sauter mean diameter (d32) of the entrained liquid droplet size distribution. The Sauter mean diameter can be converted to the volume median diameter, dv50, which is used most often in the droplet size distribution functions. There are a number of other correlations to predict droplet sizes of entrained liquid that have been developed over the years. Most of this work has been focused on annular flow conditions.
Eq. 3, developed by Kataoka et al. (1983), can be used to estimate dv50 , the volume median diameter.
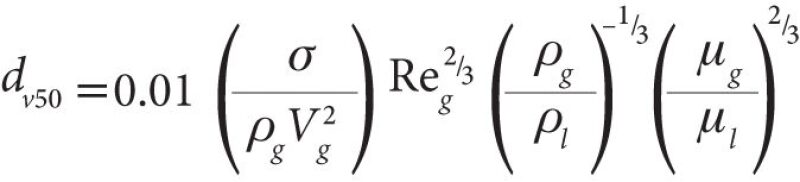
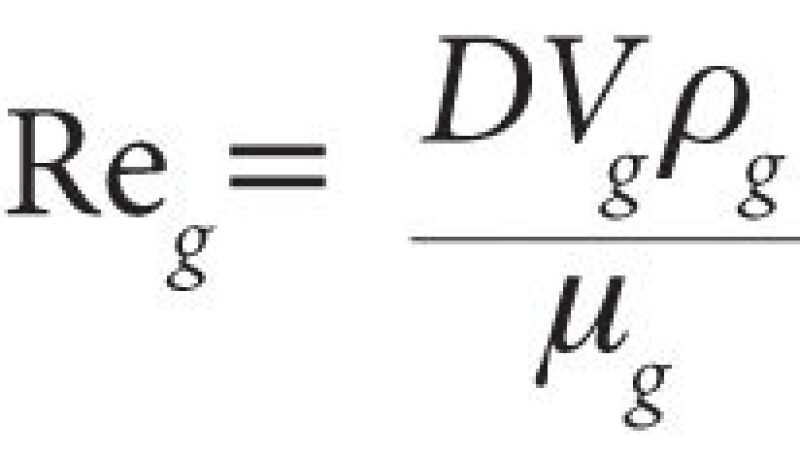
......................................................................................... (3)
The volume median diameter (dv50) is defined as the value where 50% of the total volume of droplets is made up of droplets with diameters larger than the median value, and 50% are smaller than the median value. The maximum droplet size is typically in the range of 3 to 5 times the dv50 value.
As can be seen from Eq. 3, droplet size decreases with increasing gas velocity, increasing gas density and decreasing liquid surface tension. Typical surface tension values for various liquids are shown in Table 1.
Upper-Limit Log Normal Distribution
Kataoka (1983) and Simmons and Hanratty (2001) have found the upper-limit log normal distribution to represent droplets entrained in two-phase flow.
The normalized volume frequency distribution is given by the following equations:

.......................................................................................... (4)
The values of a, δ and dmax are obtained from experimental droplet size measurement data. Typical values for these parameters are given below (Pan and Hanratty):
a = 4.0 (dmax = 5.0 dv50)
δ = 0.72
The dv50 value can be obtained from Eq. 3.
Integrating the volume frequency distribution function results in the cumulative volume distribution given as:
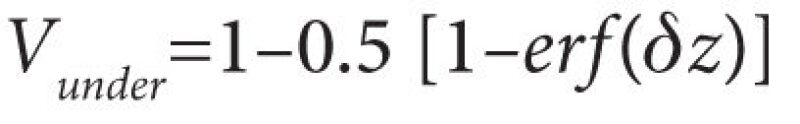
.......................................................................................... (5)
where erf(x) is the error function, which is often used in probability- and statistics-related problems (Table 2). Values of erf(x) are typically available in table or chart form and are also available as a function in Excel.
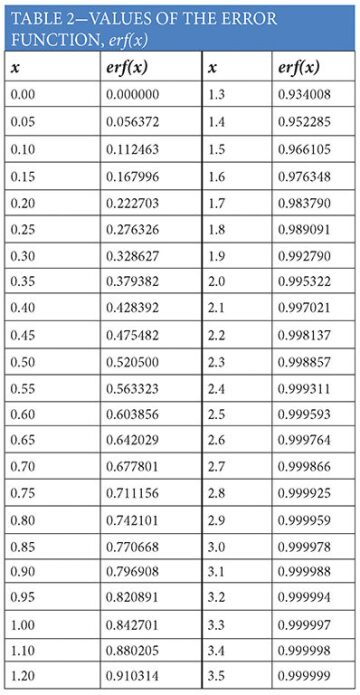
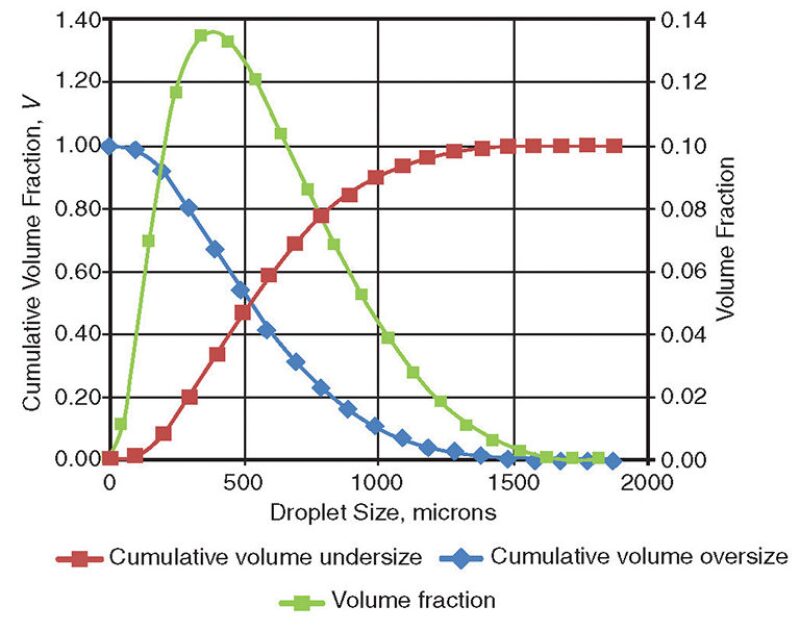
Fig. 7 is an example of the entrainment droplet size distribution for a given set of feed pipe operating conditions.
Inlet Device
The main function of an inlet device (Fig. 8) is to improve separation performance, which is achieved in the following ways:
1. Maximization of gas/liquid separation efficiency based on inlet feed conditions
2. Minimization of droplet shearing
3. Provision of good downstream velocity distributions in the separated phases
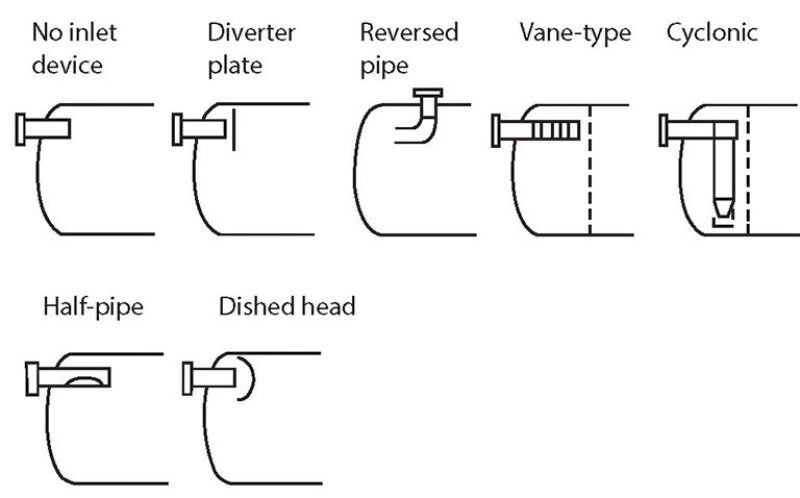
In newer, large-capacity separators, the vane-type and cyclonic inlet devices are more commonly being used. The simpler—and less expensive—impact or diverter plates are still used on smaller, less critical separation applications. The half-pipe inlet is simple and inexpensive and provides relatively good all-round performance. Table 3 shows typical qualitative performance guidelines for different inlet devices.
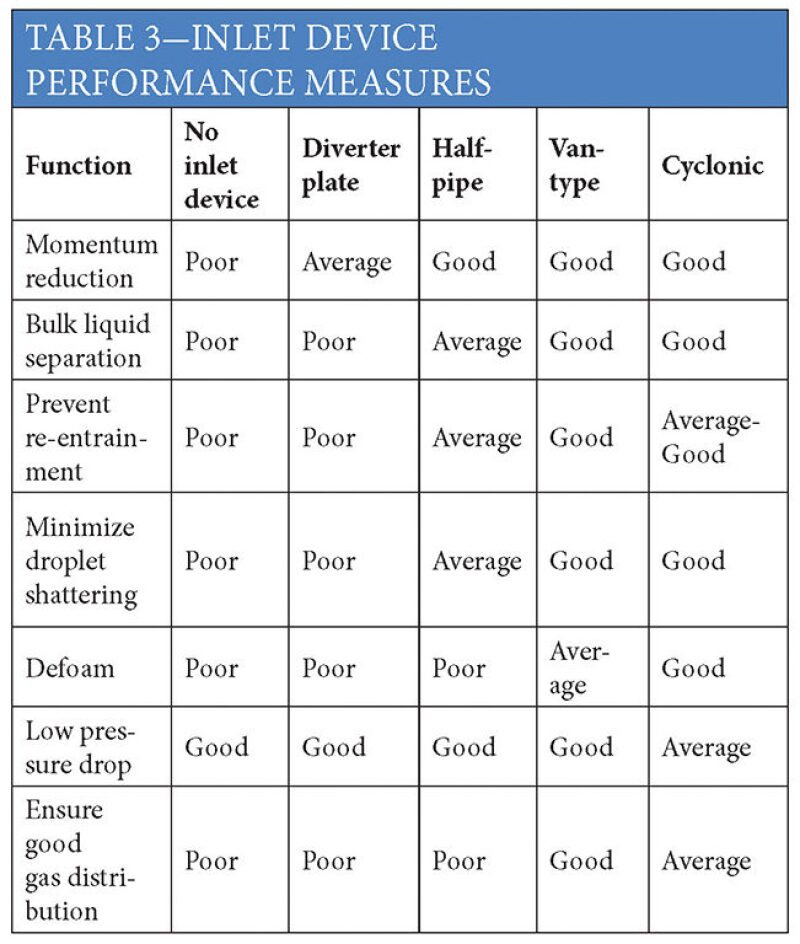
Inlet Momentum
Inlet devices are typically selected and sized based on the inlet momentum (sometimes referred to as dynamic pressure) of the separator feed stream. The intent is to reduce the energy/velocity of the feed fluids to provide conditions favorable for phase separation. Inlet momentum is defined as:
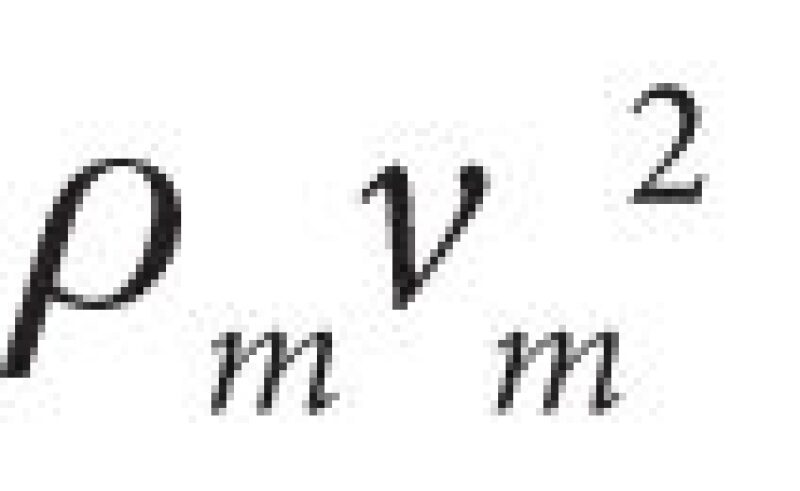
.......................................................................................... (6)
Table 4 shows typical design values (limits) for inlet momentum for various inlet devices.
Correlation of inlet momentum values (ρV2) with the performance characteristics for the various inlet devices as shown in Table 4 is imprecise at best, and the suggested limits on ρV2 are not meant to represent desired values, but upper limits. The following discussion provides an approximate attempt to quantify two of the primary performance attributes of the various inlet devices: overall liquid separation efficiency and quality of flow distribution.
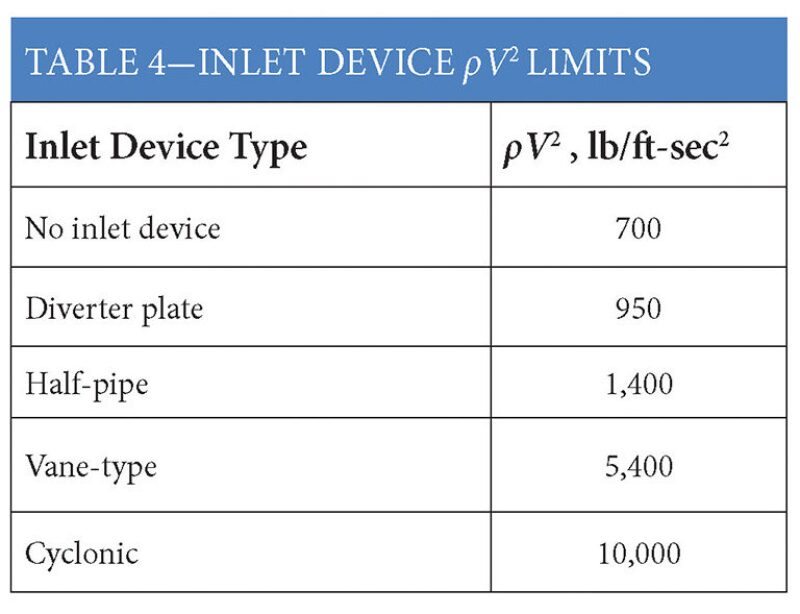
While it may not always be practical to avoid higher feed pipe velocities and corresponding ρV2 values, it must be recognized that failure to do so will result in higher entrainment loads, smaller droplet sizes, and more difficult separation conditions.
Inlet Device Separation Efficiency
Fig. 9 has been developed from mostly anecdotal information obtained from various sources, mainly technical literature available in the public domain. However, this is an area that requires additional research and study.
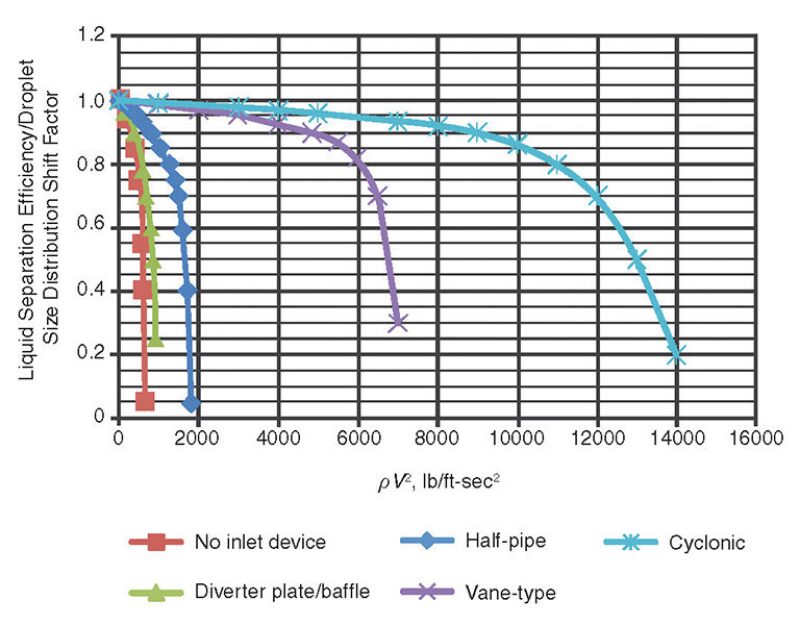
The amount of unseparated liquid as predicted by Fig. 9 is assumed to be in the form of entrained droplets immediately downstream of the inlet device (at the entry to the gas gravity separation section). The falloff in separation performance with increasing feed ρV2 reflects a larger fraction of the feed liquid in entrained droplet form, breakup of bulk liquid into droplet form, and smaller droplet sizes associated with the higher inlet velocities.
Droplet Size Distribution of Unseparated Liquid Downstream of Inlet Device
The Pan and Hanratty entrainment correlation combined with the Kataoka droplet size distribution allowed for approximate characterization of the entrainment load in the separator feed pipe. For a separator without an inlet device, which is not an uncommon situation, a simplifying assumption would be that the entrained liquid enters the gas gravity section of the separator while the nonentrained portion of the feed liquid (bulk liquid) falls into the liquid gravity section of the vessel.
However, the presence of the inlet device will modify this scenario by a) coalescing some of the inlet entrainment into the bulk liquid phase, b) causing some of the inlet bulk liquid to be re-entrained into the gas phase because of turbulence/shearing in the inlet device, and c) changing the droplet size distribution of the resultant entrained liquid exiting the inlet device. As mentioned, there is very little, if any, data available quantifying these effects. The earlier simplifying assumption regarding the overall liquid separation efficiency of the inlet device approximates the combined effect of a) and b), but does not help with c).
Corresponding to the falloff in separation efficiency with increasing inlet ρV2, it would also be expected that the droplet size distribution of the unseparated entrained liquid exiting the inlet device would be shifted to smaller sizes. There are limited to no data available that quantify this effect. Only the qualitative guidance provided in Table 3 is available. For the purposes of this work, a “droplet size distribution shift factor” will be used as indicated in Fig. 9, which should be a reasonable reflection of the droplet shattering/shearing effect of the different inlet devices.
Quality of Flow Distribution Downstream of Inlet Device
Historically, the velocity profile for the continuous phase of interest (gas, oil, or water) in a separator has been calculated from:
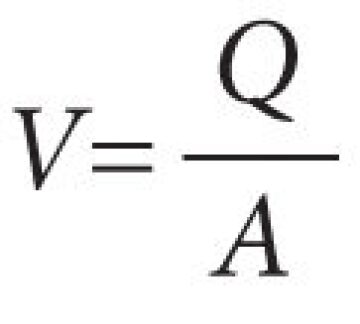
.......................................................................................... (7)
where Q is the in-situ volumetric flow rate of the continuous phase, usually in units of volume/second, and A is the cross-sectional area for flow occupied by the continuous phase. Use of this equation results in a velocity corresponding to the idealized plug flow situation. In reality, this condition is rarely, if ever, achieved, and sometimes we do not even get close.
Actual information regarding velocity profiles was, in years past, obtained from tracer surveys, which provided an approximate indication of velocity uniformity, or lack thereof, of the continuous phase of interest. In more recent years, the use of computational fluid dynamics (CFD) has provided more insight and a better definition of the flow behavior of fluids inside separation equipment. CFD has provided the basis for significant improvements in separator and separator internals design (Fig. 10).
If fluid velocity profiles are anticipated to be highly nonuniform, it is now common practice to install specifically designed internals to straighten out the velocity profile of the given continuous phase(s). Examples include perforated plates, straightening vanes, and components that resemble structured packing as used in fractionating columns. Some of these components are also intended to help promote droplet coalescence or foam collapse to improve separation performance and/or reduce separator size. Caution should be used when considering coalescing internals in production separators, as they have a tendency to become plugged (for example, with sand and wax) over time. These internals will be discussed further in the second part of this series.
Other than the qualitative guidance provided in Table 3 and scattered information obtained from published CFD studies, there is little quantitative information available on the quality of the flow distribution (gas or liquid phase) at the exit of the inlet device. This information is required to perform the droplet settling calculations for the gas gravity separation section (and to a lesser extent, for the liquid gravity separation section) downstream of the inlet device.
Fig. 11 shows the assumptions regarding the effect of the selected inlet device on downstream velocity profiles that are used in this analysis. There are two components:
1. The quality of the flow distribution immediately upon exit of the inlet device (L/Di = 0).
2. The development of the flow profile with distance downstream of the inlet device.
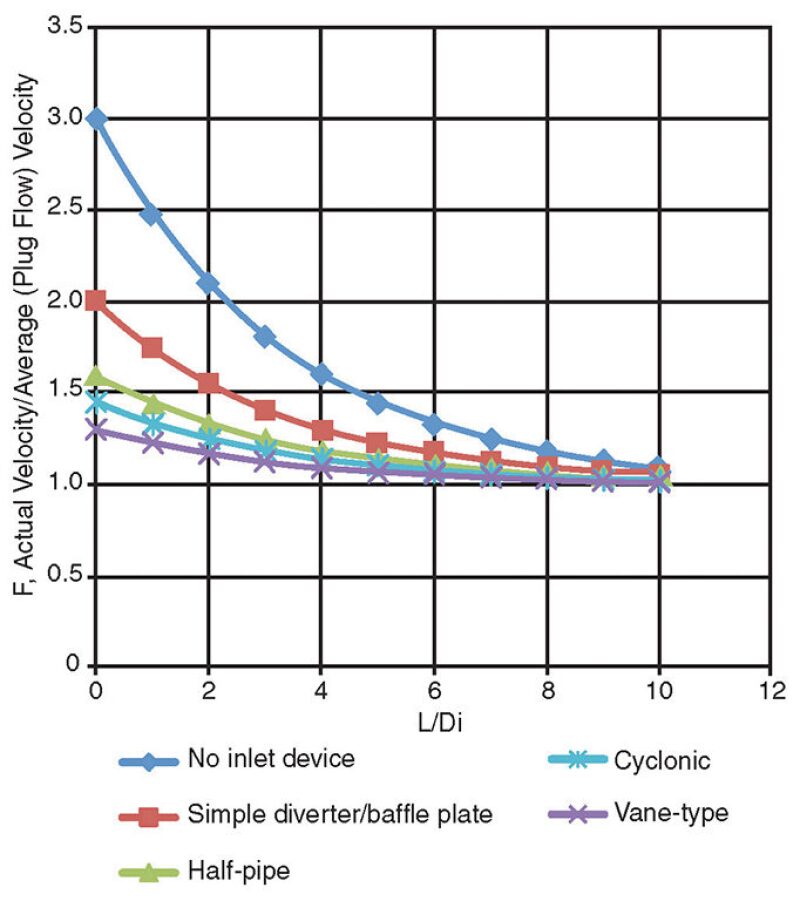
The quality of the flow distribution is characterized by the factor F, the actual average velocity/ideal plug flow velocity. F values greater than 1.0 imply unused cross-sectional flow area. Use of this factor will allow estimation of the effective actual velocity, which can then be used in the droplet settling calculations for the gas (and liquid) gravity sections. Note also that the calculated effective actual velocity for the gas gravity section will be the entrance velocity to the mist extractor section.
The separation performance of inlet devices is another area that requires more research.
The next article in the series will discuss performance quantification of the gas gravity separation, mist extraction, and liquid gravity separation sections.
For Further Reading
Ishii, M. and Grolmes, M.A. 1975. Inception Criteria for Droplet Entrainment in Two-Phase Concurrent Film Flow. AIChE J. 21 (2): 308–318.
Kataoka, I., Ishii, M., and Mishima, K. 1983. Generation and Size Distribution of Droplets in Gas-Liquid Annular Two-Phase Flow. ASME Journal of Fluids Engineering 105 (2): 230–238.
Mandhane, J.M., Gregory, G.A., and Aziz, K. 1974. A Flow-Pattern Map for Gas-Liquid Flow in Horizontal Pipes. Int. J. Multiphase Flow 1 (4): 537–553.
Pan, L. and Hanratty, T.J. 2002. Correlation of Entrainment for Annular Flow in Horizontal Pipes. International Journal of Multiphase Flow 28 (3): 385–408.
Simmons, M.J.H. and Hanratty, T.J. 2001. Droplet Size Measurements in Horizontal Annular Gas-Liquid Flow. Int. J. Multiphase Flow 27 (5): 861–883.
Mark Bothamley is the technical director and chief engineer of John M. Campbell Training and a consultant at John M. Campbell Consulting. His experience covers the areas of design, operation, troubleshooting, and optimization of offshore and onshore oil and gas production and treating facilities. Before joining the company, he served with BP/Amoco for 24 years in several locations around the world. He is a member of the SPE Separations Technology Technical Section, past specialty coordinator/chairman of the SPE Facilities and Construction Subcommittee, and a former member of the GPSA Data Book Editorial Review Board. He holds a BS in chemical engineering from Lakehead University in Canada and a diploma in natural gas and petroleum technology from the British Columbia Institute of Technology in Canada.


