Informally, decision making can be thought of as the process of “choosing the course of action that best fits the goals.” Easy? This apparently simple statement raises a number of questions such as: What, and whose, are the “goals”? Have you missed good alternatives? How do you measure “fit”? How do you define “best”?
Some decisions are “no-brainers”—for example, when you are asked whether you would like 100 dollars, no-strings-attached, or deciding which groceries to buy at the supermarket. However, the no-brainers are exceptions. Most of the important decisions we face in life are hard—complex with uncertain outcomes and consequences—with no obvious or easy solution. Adding to the difficulty, they won’t affect only you. They often affect your family, your employer, your colleagues, your friends, and others. Making good decisions, therefore, offers the opportunity to improve the quality of your personal and professional life. In short, the ability to make good decisions is a fundamental life skill.
Psychologists and behavioral scientists have demonstrated that good decision making is not a natural ability, “wired-in” following some evolutionary design. Choosing wisely is a skill, which like any other skill can be improved through learning. Unfortunately, despite its importance, few of us ever receive any training in it. We are left to learn from experience. But experience is expensive, poorly focused, and can introduce bad habits along with good ones. A better way to improve your decision-making skills is to use consistently a set of clear and logical steps for balancing the factors that influence a decision. This process is called decision analysis. However, decision analysis is not just a process; it offers a number of tools to help you execute that process.
DECISION ANALYSIS
First, we must be clear about what a decision is, and second, be clear about what it means to make a good decision.
A decision is a conscious, irrevocable, allocation of resources, not a mental commitment to follow a particular course of action. This does not mean that a decision can never be changed. Some decisions, such as drilling a well, are truly irrevocable. Others, such as entering into a partnership with another company, can be revoked, but only at some cost.
A good decision is one that is logically consistent with the decision maker’s beliefs, alternatives, and preferences (Bickel and Bratvold 2007; Bratvold et al. 2002). A good outcome is a result that is highly valued by the decision maker. Unfortunately, good decisions do not always produce good outcomes. For example, drilling a particular exploration well may be a very good decision, but still result in a dry hole. Likewise, poor decisions may be followed by good outcomes.
Uncertainty is the main underlying reason why we can have good decisions and bad outcomes (or vice versa). Like it or not, acknowledge it or not, uncertainty is an important element of most decisions. Probability is the language of uncertainty. It enables us to assess, and reason logically about, our level of knowledge. It therefore plays an important role in decision analysis. Unfortunately, even the brightest people are bad at reasoning under uncertainty and are seduced into using “rules of thumb” that cause us to fall prey to a number of errors (Welsh et al. 2005).
Decision analysis is a proven, systematic procedure for making good decisions. Its goal is to provide sufficient insight to make the best choice clear. Every activity pursued by the decision analyst should be undertaken with this in mind. For example, the generation of model results or economic metrics is not the end product of a decision analysis. Rather, the purpose of engineering analysis should be a “knowing what to do” on the part of the decision maker, and it should be sufficiently compelling to engage the support of those responsible for its implementation.
It is also important to stress what decision analysis is not. Decision analysis is not about what to choose but about how to choose. Furthermore, decision analysis is not a procedure whereby one builds large, detailed models and places probability distributions on every input, in an effort to determine the probability distribution of some output. This is in fact an abdication of responsibility, as the “decision analyst” no longer needs to think carefully about the decision problem and identify the most important uncertainties—those whose potential reduction could cause the decision to change. A case in point is the increase in computing power, by a factor of 100 million, that has taken place since the inception of decision analysis in the late 1960s. We do not believe that decision-making quality has increased in tandem. In our opinion, the clarity of recommendations may have decreased with the adoption of sophisticated probabilistic analyses that fail to give the decision makers insight into the key aspects of their problem. Decision analysis is also not a cookbook or series of boxes that must be checked before a project is approved. This is perversion of the original intent, serving only to give an illusory sense of “due diligence.”
That being said, a systematic process can facilitate insight generation. A decision-analytic framework that we find particularly useful and relevant to the current discussion is shown in Fig. 1.
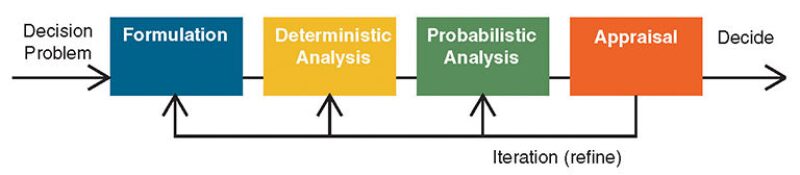
Formulation. Frame or bound the decision problem, identify the alternatives and uncertainties, decide how to quantify value, and roughly assess probabilities. This step is very important as it sets the context for all that follows.
Deterministic analysis. Roughly assess uncertainties (P10, median, and P90) and identify key uncertainties through the application of various sensitivity analyses, such as “tornado diagrams.”
Probabilistic analysis. Assess probability distributions, including dependencies, for the key uncertainties. Assess risk attitude.
Appraisal. Analyze sensitivity to probability, to determine whether changes to some set of assessments could change the optimal action. Calculate the value of gathering additional information. Determine the best alternative.
The decision-analysis cycle is iterative. If further assessments are required or profitable information-gathering programs exist, then this information should be gathered and the cycle repeated. Otherwise, the decision should be made. The decision model is complete when further refinements are not expected to change the recommended course of action. This is quite different from many “study-based” processes that we have observed. First, study-based methodologies tend to be linear—great detail is built into the model from the start rather than adding detail in important areas when justified. (Begg et al. 2001). The results of this model (e.g., a reservoir model) are then passed to the next technical discipline (e.g., facilities), and so on. No accommodation for learning or refinement is included. Second, there is no stopping rule when performing a study or making a forecast—which can always be made a bit better. Finally, the decision-analysis cycle is decision-focused rather than valuation-focused. This subtle distinction is critical. A value focus seeks to determine the absolute value of each alternative, rather than its relative value, as with a decision focus. Recall, the goal is to make a good decision, which only requires that one identify which alternative is the best—not its value per se. One can be clear about what to do, but still not be certain of what will happen.
UNCERTAINTY QUANTIFICATION AND REDUCTION
There has been a lot of focus on uncertainty quantification and reduction in the E&P industry for the past couple of decades. In this context, it is important to recognize that uncertainty quantification or reduction is not necessary for good decision making.
Uncertainty reduction creates no value unless it holds the potential to change the decision. We observe that many professionals fail to critically assess this issue, assuming that uncertainty reduction is a desirable goal at almost any cost. For example, suppose you recently entered a drawing for a free trip to Hawaii from a very reputable company. You have just been told that you won and you can take the trip anytime during the next year. Should you decide to claim the prize? Sure. Why not? But, are you certain of how much you will enjoy the vacation? No. Can you imagine a scenario where you wish you would not have taken the vacation? Certainly! For example, suppose a tropical cyclone strikes the islands while you are there. Yet, it is clear that you should accept the prize. So, here is a situation where we must make a decision under uncertainty, but the best course of action is clear. Or, consider this example. Suppose your company is considering drilling a well whose value is uncertain; there is an 80% chance it could be worth USD 10 million after drilling costs, and a 20% chance it could be worth USD 100 million. The outcome is highly uncertain, but the decision to drill is clear. Reducing this uncertainty cannot alter the best course of action.
We often hear people in the industry speak of reducing uncertainty by building a model. Modeling uncertainty does not reduce it. Rather, the model is an explicit representation of the uncertainty that is already implicit in the decision problem. Uncertainty can only be reduced or altered by our choices—not simply our decision to recognize it formally.
Uncertainty without a decision is simply a worry. Once the decision is clear, further quantification (or reduction) of uncertainty is a waste of resources—unless it could influence subsequent decisions. Suppose you own your own home, which is your most significant financial asset. Do you carry fire insurance? Probably. Before purchasing this insurance did you build a model to better estimate the chance your home would be destroyed by fire? No. Could you have done this? Sure. Then why didn’t you? Because for most of us, there is no decision to be made; our mortgage contract requires that we carry fire insurance. No alternatives = no decision, and thus, no need to quantify uncertainty.
COGENCY VS. VERISIMILITUDE
Finally, we need to say a few words about model complexity. In our experience, companies tend to build too much detail into their decision-making models from the start and focus too much on specific cases or inputs that don’t influence the decision. A distinction that we have found useful is cogency vs. verisimilitude (Bickel and Bratvold 2007). Cogency is having the property of being compelling. Verisimilitude means being true to life. We seek cogent decision models, rather than models exhibiting verisimilitude. Ron Howard, one of the founders of decision analysis, has proposed a very helpful analogy to explain this concept. Consider model-train building. What makes a very good model train? One that is true to life. For example, an average model train might include a bar car. A good model train might include a bar car with people. A very good model train might show the people holding drinks. In an award-winning model train, you would be able to tell what kind of drinks the people were holding—for example, martinis with olives. Yet, inside a world-class model train, you would be able to see the pimiento inside the olive!
Decision analysis is not about building model trains. Rather, we seek to provide insights to decision makers regarding critical decisions. Rarely does this require “pimiento-level” modeling detail. This level of modeling detail is really a shirking of responsibility on the part of the decision analyst, who either will not or cannot exercise judgment and build a model that includes only the most salient factors. Building in detail is easy. Building in incisiveness is hard work. As Howard has written, …the real problem in decision analysis is not making analyses complicated enough to be comprehensive, but rather keeping them simple enough to be affordable and useful.
References
Begg, S.H. Bratvold, R.B. and Campbell, J.M. (2001). Improving Investment Decisions Using a Stochastic Integrated Asset Model. Paper SPE 71414 presented at the SPE Annual Technical Conference and Exhibition, New Orleans.
Bickel, J.E. and Bratvold, R.B. 2007. Decision Making in the Oil and Gas Industry: From Blissful Ignorance to Uncertainty-Induced Confusion. Paper SPE 109610 presented at the SPE Annual Technical Conference and Exhibition, Anaheim, California, 11–14 November. DOI: 10.2118/109610-MS.
Bratvold, R.B., Begg, S.H., and Campbell, J.M. 2002. Would You Know a Good Decision if You Saw One? Paper SPE 77509 presented at the SPE Annual Technical Conference and Exhibition, San Antonio, Texas, 29 September–2 October. DOI: 10.2118/77509-MS.
Welsh, M.B., Bratvold, R.B., and Begg, S.H. 2005. Cognitive Biases in the Petroleum Industry: Impact and Remediation. Paper SPE 96423 presented at the SPE Annual Technical Conference and Exhibition, Dallas, 9–12 October. DOI: 10.2118/96423-MS.

| Reidar B. Bratvold is a professor at the University of Stavanger, Norway. His teaching and research interests are on representing and solving decision problems in E&P, real option valuation, portfolio analysis, and behavioral challenges in decision making. He has twice served as SPE Distinguished Lecturer and is the author, together with Steve Begg, of an upcoming SPE primer on it. Bratvold has held various executive positions in the oil-services industry and engineering positions with IBM and Statoil. He spent his early working years as an oil roughneck in the North Sea. Bratvold holds a PhD degree in petroleum engineering and an MSc degree in mathematics from Stanford University, and completed further studies in business and management science education at the Institut Européen d’Administration des Affaires (INSEAD)and Stanford University. He has been elected into the Norwegian Academy of Technological Sciences. |

| Steve Begg is a professor of Petroleum Engineering and Management at the Australian School of Petroleum, University of Adelaide. His focus is on improved decision-making tools and processes, including asset and portfolio economic evaluation, and the psychological aspects of eliciting expert opinions and uncertainty assessments. Begg has been director of Decision Science and Strategic Planning with Landmark, has held a variety of senior operational engineering and geoscience positions with BP Exploration, and before that led BP’s reservoir characterization research team. He has BSc and PhD degrees in geophysics from the University of Reading, UK. |

